Persamaan Garis Lurus
Persamaan garis lurus adalah persamaan matematika yang memiliki grafik berupa garis lurus
A. Bentuk Umum dan Grafik
Bentuk Umum
y = mx + c atau Ax + By + C = 0 dengan m, A, B, dan C adalah bilangan real
Contoh persamaan garis lurus:
1. y = 3x + 6
2. 3x + 5y + 10 = 0
3. 3y = x - 4
4. 2x = 5y + 6
Contoh yang bukan persamaan garis lurus
1. 
2.  =0
=0
Bentuk Grafik
Contoh:
1. Bentuk grafik persamaan x - 5y = 10 adalah ....
jawab:
⇨tentukan titik potong dengan sumbu X
jadikan y = 0 ⇨ substitusikan y = 0 ke x - 5y = 10
x - 5(0) = 10 => x - 0 = 10 => x = 10
diperoleh titik potong persamaan dengan sumbu X yaitu (10, 0)
⇨ tentukan titik potong dengan sumbu Y
jadikan x = 0 ⇨ substitusikan x = 0 ke x - 5y = 10
0 - 5y = 10 => -5y = 10
y =

=> y = -2
diperoleh titik potong persamaan dengan sumbu Y yaitu (0, -2)
⇨pada grafik kartesius hubungan titik (10, 0) dan (0, -2) dengan sebuah garis lurus
B. Gradien/ Kemiringan garis
simbol gradien = m
rumus-rumus mencari gradien (m)
1. y =mx + c 👉 m = nilai gradien
2. Ax + By + C = 0 👉 m = 
3. jika diketahui garis melalui 2 titik (x1, y1) dan (x2, y2) 👉 m = 
Contoh:
1. Tentukan gradien (m) pada persamaan berikut:
a. y = 3x + 7
b. 5x - y + 12 = 0
c. 2y + 3x - 6 = 0
d. persamaan garis yang melalui (2, -5) dan (-1,0)
Jawab:
1. a. y = 3x + 7
⇨ingat rumus y = mx + c, dimana m = nilai gradien 👉 m = 3
b. 5x - y + 12 = 0
⇨ingat pada bentuk persamaan Ax + By + C = 0, nilai m = 
maka A= 5, B= -1 👉 m = 
m =  => m = 5
=> m = 5
c. 2y + 3x - 6 = 0 ⇒ A=3, B=2
👉 m =  => m =
=> m = 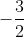
d. persamaan garis yang melalui (2, -5) dan (-1,0) 👉 m = 
(x1, y1) => (2,-5) => x1=2 dan y1=-5
(x2, y2) => (-1,0) => x2=-1 dan y2=0
⇨ m =

=> m =

m=

C. Menentukan Persamaan Garis Lurus
1. Jika diketahui nilai m dan 1 koordinat titik sembarang (x1, y1) 👉 y - y1 = m(x - x1)
Contoh:
1. persamaan garis yang melalui (5, -2) dan bergradien -3 adalah ....
jawab:
(x1, y1) => x1 = 5 dan y1 = -2
m = -3
⇨ y - y1 = m(x - x1) => y - (-2) = -3(x - 5)
y + 2 = -3x + 15 ⇨ y = -3x + 15 - 2
y = -3x + 13 => 3x + y = 13
∴ persamaan garis yang melalui (5, -2) dan bergradien -3 adalah 3x + y = 13
2. persamaan garis yang melalui (5, -2) dan bergradien
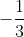
adalah ....
jawab:
(x1, y1) => x1 = 5 dan y1 = -2
m =
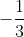
⇨y - y1 = m(x - x1)
⇨

⇨

⇨ 3(y+2) = -1(x-5) => 3y + 6 = -x + 5
x + 3y + 1 = 0
∴ persamaan garis yang melalui (5, -2) dan bergradien
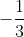
adalah
x + 3y + 1 = 0
2. Jika diketahui melalui dua titik (x1, y1) dan ((x2, y2) 👉 
Contoh:
1. Persamaan garis yang melalui titik (2, -5) dan (-1,0) adalah ....
Jawab:
(x1,y1) = (2, -5) ⇒ x1 = 2 dan y1 = -5
(x2,y2) = (-1, 0) ⇒ x2 = -1 dan y2 = 0
⇨ 
⇨ 
⇨ 
⇨ -3(y + 5) = 5(x-2)
👉 -3y - 15 = 5x - 10 👉 5x + 3y - 5 = 0
3. Pada grafik garis lurus
Contoh:
1. Perhatikan garis k pada gambar berikut adalah ....
a = 5, b= 8 👉 ax + by = ab
👉 5x + 8y = 5.8 👉 5x + 8y = 40
∴ persamaan garis k adalah 5x + 8y = 40
D. Hubungan antar 2 persamaan garis lurus
hubungan antar 2 persamaan garis lurus dilihat berdasarkan nilai gradiennya (m), yaitu:
1. saling sejajar → garis 1 // garis 2
👉 m1 = m2
2. saling tegak lurus → garis 1 ⊥ garis 2
👉 m1 × m2 = -1
Contoh:
1. Tentukanlah persamaan garis berikut saling sejajar atau saling tegak lurus adalah ...
A. y = -5x + 4 dan x + 5y + 10 = 0
B. y = -3x + 5 dan 6x + 2y + 8 = 0
C. y = -4x + 2 dan 2x - 8y + 16 = 0
D. -3x = y + 6 dan 4x - 12y - 12 = 0
gunakan rumus mencari gradien pada persamaan garis, yaitu
y =mx + c 👉 m = nilai gradien dan
Ax + By + C = 0 👉 m =

⇨ dua garis saling sejajar maka kedua garis tersebut memiliki gradien yang sama, yaitu m1 = m2
⇨ dua garis saling tegak lurus maka hasil perkalian gradien tersebut adalah -1 yaitu m1 ⨉ m2 = -1
A. y = -5x + 4 👉 m1 = -5 dan
x + 5y + 10 = 0 👉 m2 =

m1 ≠ m2 ⇒ tidak sejajar dan
m1 ⨉ m2 ≠ -1 ⇒ tidak tegak lurus
B. y = -3x + 5 👉 m1 = -3 dan
6x + 2y + 8 = 0 👉 m2 =

👉 m2 = -3
m1 = m2 ⇒ saling sejajar
C. y = -4x + 2 👉 m1 = -4 dan
2x - 8y + 16 = 0 👉 m2 =

👉 m =

m1 ≠ m2 ⇒ tidak sejajar dan
m1 ⨉ m2 = -1 ⇒ saling tegak lurus
D. -3x = y + 6 👉 m1 = -3 dan
4x - 12y - 12 = 0 👉 m2 =

👉 m =

m1 ≠ m2 ⇒ tidak sejajar dan
m1 ⨉ m2 = -1 ⇒ saling tegak lurus
E. Menentukan persamaan garis lain
CARA I
1. tentukan gradien persamaan garis yang diketahui berdasarkan hubungan antar garis
a. jika saling sejajar ⇒ gradien kedua garis sama ⇒ m1 = m2
b. jika saling tegak lurus ⇒ hasil perkalian gradien kedua garis = -1 ⇒ m1 ⨉ m2 = -1
2. tentukan persamaan garis yang diminta menggunakan rumus y - y1 = m(x - x1)
CARA II
1. dua garis saling sejajar
persamaan garis 1 melalui (x1, y1) // garis 2 ≡ Ax + By = C
⇨ persamaan garis 1 ≡ Ax + By = Ax1 + By1
2. dua garis saling tegak lurus
persamaan garis 1 melalui (x1, y1) ⊥ garis 2 ≡ Ax + By = C
⇨ persamaan garis 1 ≡ Bx - Ay = Bx1 - Ay1
Contoh:
1. Persamaan garis yang melalui titik P(-3,2) dan sejajar dengan y - 3x - 12 = 0 adalah ....
Jawab:
CARA I
garis 1 melalui (x1, y1) ⇒ x1 = -3 dan y1 = 2 // garis 2 ≡ y - 3x - 12 = 0 ⇒ m2 = 3
karena saling sejajar maka m1 = m2 ⇒ m1 = 3
⇨ Persamaan garis 1
y - y1 = m1(x - x1)
y - 2 = 3(x - (-3))
y -2 = 3(x+3)
y-2 = 3x + 9
y = 3x + 11 atau 3x - y + 11 = 0
Persamaan garis 1melalui titik P(-3,2) // garis 2 ≡ y - 3x - 12 = 0 atau -3x + y - 12 = 0
⇓
Ax + By = Ax1 + By1
⇨ -3x + y = -3(-3) + 1(2)
⇨ -3x + y = 9 + 2
⇨ 3x - y + 11 = 0
=0
=> m = 5
=> m =








Posting Komentar
0 Komentar