HIMPUNAN
A. Pengertian
Himpunan adalah kumpulan benda atau obyek yang didefinisikan dengan jelas/dapat diukur. Benda/objek dalam himpunan disebut elemen atau anggota himpunan
Contoh himpunan
- Kumpulan binatang berkaki empat
- himpunan bilangan prima antara 0 dan 20
- kumpulan presiden negara Asia Tenggara
Contoh bukan himpunan:
- kumpulan binatang yang lucu
- kumpulan gunung-gunung yang tinggi
- sekelompok siswi cantik
B. Notasi Himpunan, Anggota Himpunan dan Bilangan Kardinal
1. Notasi himpunan
Himpunan dinotasika dengan huruf kapital (A, B, C, D,...) diikuti tanda sama dengan "=" dan untuk menuliskan anngota himpunan diawali dan diakhiri kurung kurawal.
Contoh:
P = {1, 2, 3, 4}
Q = {warna lampu lalu lintas}
2. Anggota himpunan
anggota suatu himpunan dinotasikan ∈ dan jika bukan anggota suatu himpunan ∉
1. 3 ∈ P
2. 0 ∉ P
3. merah ∈ Q
4. hijau ∈ Q
5. orange ∉ Q
3. Bilangan kardinal
adalah bilangan yang menyatakan banyaknya anggota suatu himpunan
n(P) = 4
n(Q) = 3
C. Cara Menuliskan Himpunan
1. Deskripsi
adalah cara menyatakan suatu himpunan dengan kata-kata
A={bilangan asli ganjil antara 0 dan 10}
2. Notasi pembentuk himpunan
adalah cara menyatakan suatu himpunan dengan notasi dan batasan.
A = {x| 0 < x < 10, x ∈ bilangan asli ganjil}
3. Tabulasi
adalah cara menyatakan suatu himpunan dengan mendaftarkan anggotanya satu per satu
A={1, 3, 5, 7, 9}
D. Himpunan Kosong, Himpunan Hingga, Himpunan Tak Hingga
1. Himpunan Kosong
adalah himpunan yang tidak mempunyai anggota, atau memiliki bilangan kardinal 0
dinotasikan dengan { } atau Ø
Contoh:
B = {bilangan prima yang kurang dari 2} ⇒ n(B) = 0
K = {nama bulan yang diawali huruf B} ⇒ n(K) = 0
2. Himpunan Hingga
adalah himpunan yang memiliki anggota dengan jumlah tertentu.
Contoh:
A = {a, i, u, e, o} ⇒ n(A) = 5
B = {bilangan bulat antara -2 dan 10}
= {-1,0,1,2,3,4,5,6,7,8,9} ⇒ n(B) = 11
3. Himpunan Tak Hingga
adalah himpunan yang memiliki anggota tak hinggga (tak terbatas)
Contoh:
B = {bilangan bulat}
= { ..., -2, -1, 0, 1, 2, 3, 4, ...} ⇒ n(B) = ∽
E. Himpunan Sama dan Himpunan Ekuivalen
1. Himpunan Sama
- adalah dua himpunan atau lebih yang memiliki anggota sama dan banyaknya anggota sama banyak
- dinotasikan: =
Contoh:
1. Diketahui himpunan-himpunan berikut:
A={k, a, o, s}
B={s, o, a, k}
C={t, o, a, s}
diantara himpunan tersebut yang himpunan yang sama adalah ....
Jawab:
A = B ⇒ karena anggota dan banyaknya anggota dikedua himpunan tersebut sama
2. Himpunan Ekuivalen
- adalah dua himpunan atau lebih himpunan yang banyak anggotanya sama banyak.
- dinotasikan: ∽
Contoh:
1. Diantara himpunan berikut yang saling ekuivalen adalah ....
P = {a, i, u, e, o}
Q = {m, u, r, k, a}
R = {s, a, n, t, u, y}
Jawab:
P ∽ Q ⇒ karena banyak anggota dikedua himpunan tersebut sama
F. Himpunan Semesta dan Diagram Venn
1. Himpunan Semesta
adalah himpunan yang memuat seluruh anggota yang dibicarakan.
Notasi = S
2. Diagram Venn
adalah diagram yang digunakan untuk menggambarkan hubungan antara dua atau lebih himpunan
Contoh:
Gambarkan dalam diagram venn hubungan himpunan berikut
S = {0, 1, 2, 3, 4, 5, 6, 7, 8,9, 10}
A = {2, 3, 5, 7}
B = {1,2, 3, 4, 6}
jawab:
Diagram Venn
G. Himpunan Bagian dan Himpunan Kuasa
1. Himpunan Bagian
- Himpunan A bagian dari himpunan B, jika setiap anggota himpunan A merupakan anggota himpunan B.
- Notasi ⇒ A ⊂ B
- Himpunan kosong menjadi himpunan bagian dari semua himpunan
- Banyaknya himpunan bagian A yang mungkin adalah
dengan n(A) = banyaknya anggota himpunan A
- banyaknya himpunan bagian A yang memiliki m anggota dapat dicari menggunakan rumus
dengan: n = banyak anggota himpunan A
m = banyak anggota himpunan bagian yang dicari
Contoh:
1. Diketahui A = {p, q, r}. Tentukanlah:
a. banyaknya himpunan bagian yang mungkin dari himpunan A
b. banyaknya himpunan bagian A yang memiliki 2 anggota
Jawab:
a. banyaknya himpunan bagian yang mungkin dari himpunan A =
A = {p, q, r} ⇒ n(A) = 3
= 8
banyaknya himpunan bagian yang mungkin dari himpunan A adalah 8 himpunan
b. banyaknya himpunan bagian A yang memiliki 2 anggota ⇒ m = 2
A = {p, q, r} ⇒ n(A) = n = 3
3C2 = 3
banyaknya himpunan bagian A yang memiliki 2 anggota adalah 3 himpunan
2. Himpunan Kuasa
- himpunan kuasa A adalah himpunan yang anggotanya semua himpunan bagian A
- dinotasikan ⇒ P(A)
- banyaknya anggota himpunan kuasa himpunan n(P(A)) =
Contoh:
1. Diketahui A = {p, q, r}. Tentukanlah:
a. banyaknya anggota himpunan kuasa himpunan A
b. himpunan kuasa dari himpunan A
Jawab:
a. banyaknya anggota himpunan kuasa himpunan A
A = {p, q, r} ⇒ n(A) = 3
n(P(A)) =
= 
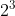
= 8
banyaknya anggota himpunan kuasa himpunan A ada 8
b. himpunan kuasa dari himpunan A
A = {p, q, r}
⇒himpunan bagian A yang memiliki 0 anggota = { }
⇒himpunan bagian A yang memiliki 1 anggota = {p},{q}, {r}
⇒himpunan bagian A yang memiliki 2 anggota = {p,q}, {p,r}, {q,r}
⇒himpunan bagian A yang memiliki 3 anggota = {p,q,r}
P(A) = {{ }, {p},{q}, {r}, {p,q}, {p,r}, {q,r}, {p,q,r}}
H. Operasi Himpunan
1. Irisan dua himpunan
- Irisan himpunan A dan himpunan B adalah himpunan yang anggotanya merupakan anggota himpunan A sekaligus menjadi anggota himpunan B
- notasi ⇒ A ⋂ B
Diketahui:
S = {1,2,3,4,5,6,7,8,9,10}
A = {faktor dari 12}
B = {faktor dari 10}
Tentukan: a. A ⋂ B
b. gambarkan dalam diagram venn
Jawab:
a. A = {1,2,3,4,6}
B = {1,2,5,10}
A ⋂ B = {1,2}
b. diagram venn
2. Gabungan
- gabungan dua himpunan A dan himpunan B adalah himpunan yang anggotanya berasal dari anggota himpunan himpunan A atau himpunan B atau anggota persekutuan himpunan A dan himpunan B
- notasi ⇒ A ⋃ B
3. Selisih
- Selisih dua himpunan A dan B adalah himpunan dari semua anggota himpunan A tetapi tidak dimiliki himpunan B
- notasi ⇒ A - B
5. Komplemen
- komplemen suatu himpunan menunjukkan anggota yang bukan himpunan tersebut namun masih termasuk anggota himpunan semesta.
- notasi ⇒ A’ atau
Posting Komentar
0 Komentar